弾性体力学

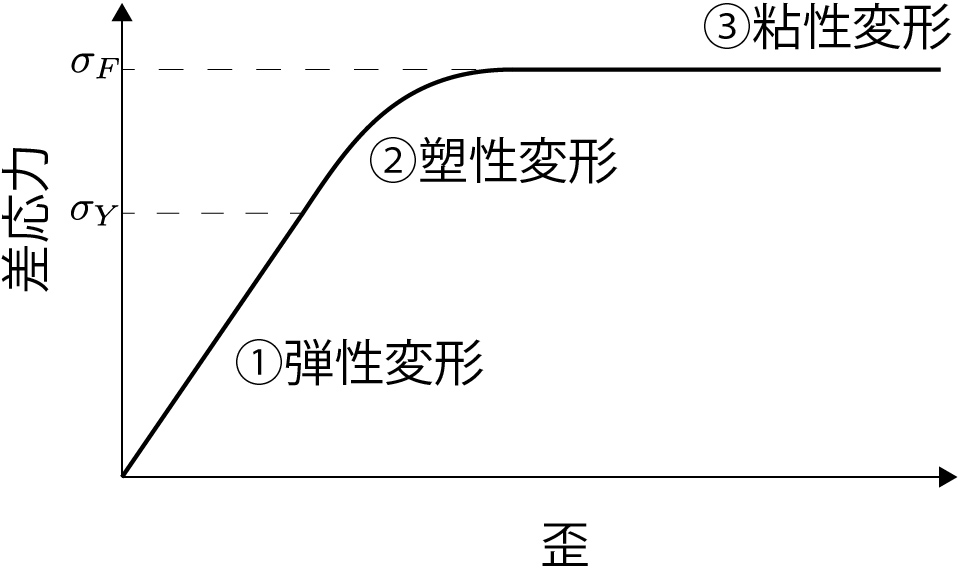
応力

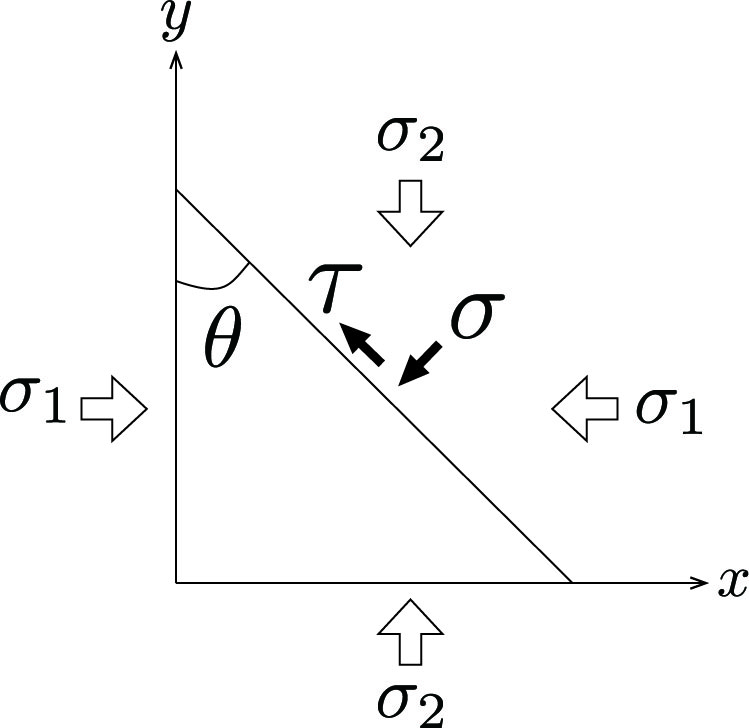
応力は単位面積に作用する力として定義される。 このとき、力はベクトル量なので、応力もベクトルである。 したがって、任意の面に応力$S$が作用している場合、$S$は面に垂直に作用する成分（$\sigma$：垂直応力）と平行に作用する成分（$\tau$：剪断応力）に分解することができる。

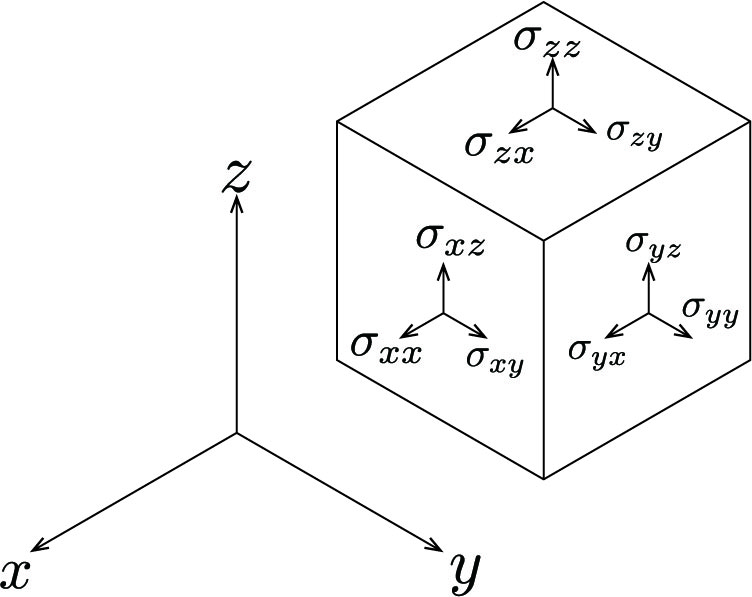
直交座標系において同様に応力を分解すると図1のようになる。垂直応力$\sigma_x$の添字$x$は応力が作用する方向を表す。 一方、剪断応力$\tau_{xy}$の最初の添字$x$は応力の作用する面の法線方向を表し、２番目の添字は応力の作用する方向を表している。 この応力は以下のように行列表記をすることができ、これを応力テンソルと呼ぶ。 \[ S=\left( \begin{array}{ccc} \sigma_x & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_y & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_z \end{array} \right) \tag{1} \]

剪断応力成分が0となるように座標系をとったときの垂直応力のことを主応力と呼ぶ。 ３つの主応力を$\sigma_1\ge\sigma_2\ge\sigma_3$になるようにとったとき、$\sigma_1$を最大主応力、$\sigma_2$を中間主応力、$\sigma_3$を最小主応力と呼ぶ。 ある座標系で、とある応力状態（$\sigma_x, \sigma_y, \sigma_z, \tau_xy, \tau_yz, \tau_zx$）が与えられたとき、 主応力は下記の式を展開した$\lambda$に関する３次方程式の根である。 \[ \mathrm{det}(\sigma-\lambda E)=\left| \begin{array}{ccc} (\sigma_x-\lambda) & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & (\sigma_y-\lambda) & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & (\sigma_z-\lambda) \end{array} \right| \tag{2} \]

弾性体が平衡状態にあるとき、応力テンソル$\sigma_{ij}$と体積力$F_i$の関係は次の式のようになる。 \[ \sigma_{ji,j}+F_i=0 \tag{3} \] 式(3)を導出するためには$(0,0,0), (dx,0,0), (dx,dy,0), (0,dy,0), (0,dy,dz), (dx,dy,dz), (dx,0,dz), (0,0,dz)$を頂点とする微小直方体を考え、各軸方向の式のつりあいを求める。

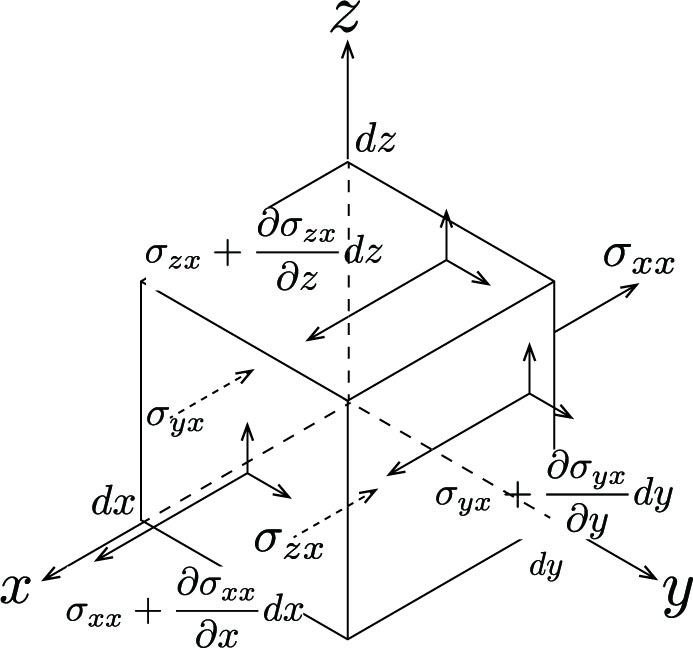
x軸方向における応力成分は図2のようになる。偏微分$\partial \sigma_{xx}/\partial x$は単位距離当たりの変化量を表す。したがって距離をかけてあれば離れた面での応力がわかる。 x軸方向の釣り合いの式は、体積力$F_x$が作用していることを考慮して、 \[ \left(\sigma_{xx}+\frac{\partial \sigma_{xx}}{\partial x}dx\right)dydz-\sigma_{xx}dydz +\left(\sigma_{yx}+\frac{\partial \sigma_{yx}}{\partial y}dy\right)dzdx-\sigma_{zx}dzdx +\left(\sigma_{zx}+\frac{\partial \sigma_{zx}}{\partial z}dx\right)dxdy-\sigma_{zx}dxdy +F_x dxdydz=0 \tag{4} \] 整理すると、 \[ \frac{\partial \sigma_{xx}}{\partial x}+\frac{\partial \sigma_{yx}}{\partial y}+\frac{\partial \sigma_{zx}}{\partial z}+F_x=0 \tag{5} \] y軸、z軸も同様で、総和規約と$\frac{\partial \sigma_{ji}}{\partial x_j}=\sigma_{ji,j} (x_1=x, x_2=y, x_3=z)$より、式(3)が求まる。

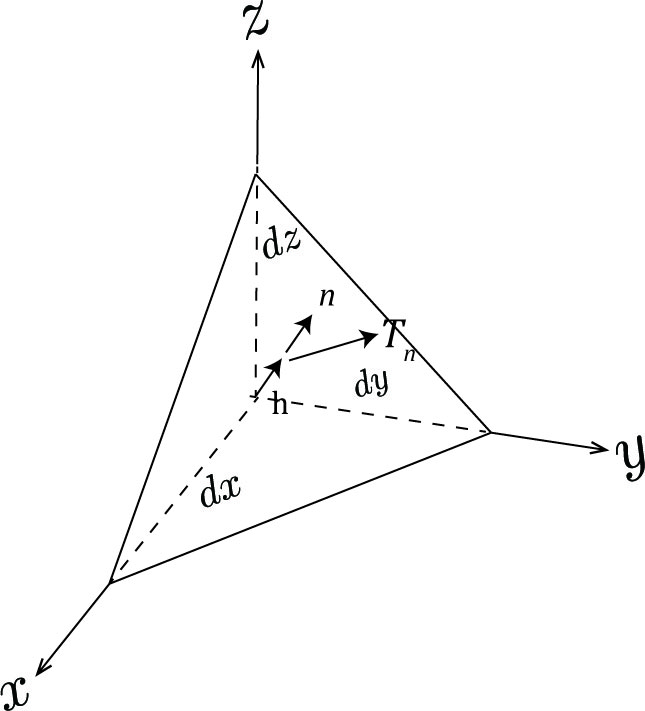
応力テンソル$\sigma_{ij}$が与えられたとき、法線ベクトルが$n$である面（面積：$dS$）に作用する応力ベクトル$T_i$は、 \[ T_i=\sigma_{ij}n_j \tag{6} \] 式(6)をコーシーの関係式と呼ぶ。微小4面体の体積は$dS\cdot h/3$なので、体積力を$F$とするとx方向にかかる体積力による力は$F_x dS\cdot h/3$となる。 また、$yz$面、$zx$面、$xy$面の面積はそれぞれ、$dS\cdot n_x$、$dS\cdot n_y$、$dS\cdot n_z$なので、微小4面体におけるx軸方向の力の釣り合いは、 \[ T^n_xdS+F_x\cdot \frac{1}{3}dS\cdot h=\sigma_{xx}dS\cdot n_x+\sigma_{yy}dS\cdot n_y+\sigma_{zz}dS\cdot n_z \tag{7} \] 微小4面体なので$h\rightarrow0$である。したがって、 \[ T^n_x=\sigma_{xx}n_x+\sigma_{yy}n_y+\sigma_{zz}n_z \tag{8} \] $y$軸、$z$軸も同様で、総和規約を用いると式(6)が求まる。

モール円

最大主応力から角度$\theta$だけ傾いた斜面をP（面積：a）とする。この面にかかる法線応力は力の釣り合いより、 \begin{align*} a\cdot \sigma&=a\cos\theta\cdot\sigma_1 \cos\theta+a\sin\theta\cdot\sigma_2 \sin\theta \\ \sigma&=\sigma_1\cos^2\theta+\sigma_2\sin^2\theta \\ &=\sigma_1 (1-\sin^2\theta)+\sigma_2\sin^2\theta \\ &=\sigma_1-(\sigma_1-\sigma_2)\sin^2\theta \\ &=\sigma_1-(\sigma_1-\sigma_2)\frac{1-\cos 2\theta}{2} \\ &=\frac{1}{2}(\sigma_1+\sigma_2)+\frac{1}{2}(\sigma_1-\sigma_2)\cos 2\theta \tag{9} \end{align*} 同様にせん断応力も、 \begin{align*} a\cdot \tau&=a\cos\theta\cdot\sigma_1 \sin\theta-a\sin\theta\cdot\sigma_2 \cos\theta \\ \tau&=\sigma_1 \sin\theta\cos\theta-\sigma_2\sin\theta\cos\theta \\ \tau&=\frac{1}{2}(\sigma_1-\sigma_2)2\sin\theta\cos\theta \\ \tau&=\frac{1}{2}(\sigma_1-\sigma_2)\sin 2\theta \tag{10} \end{align*} 式(9)と(10)は以下のように変形できる。 \begin{align*} \left(\sigma-\frac{\sigma_1+\sigma_2}{2}\right)^2&=\left(\frac{\sigma_1-\sigma_2}{2}\right)^2 \cos^2 2\theta \tag{11} \\ \tau^2&=\left(\frac{\sigma_1-\sigma_2}{2}\right)^2 \sin^2 2\theta \tag{12} \end{align*} 式(11)と(12)の両辺をそれぞれ足すことで \[ \left(\sigma-\frac{\sigma_1+\sigma_2}{2}\right)^2+\tau^2=\left(\frac{\sigma_1-\sigma_2}{2}\right)^2 \tag{13} \] が求まる。これを図示すると図５のようになる。これをモール円と呼ぶ。

弾性体の変形中、$\sigma_1$の増加に伴ってモール円の半径が大きくなっていく。モール円が式(14)で表されるクーロンの破壊基準に接すると弾性体は破壊する。 \[ \tau_f=c+\mu_i \sigma_n \tag{14} \] ここで、$c$は凝着力、$\mu_i$は内部摩擦係数である。このときの$\theta$は破壊面の角度である。

間隙水圧$p$が存在する場合、間隙水圧が封圧$\sigma_2$を支えるので、弾性体にかかる正味の応力は$\sigma_2-p$となる。したがって、図６のようにモール円は$p$だけ平行移動する。

歪

弾性体内部の変形は、任意の座標$(x, y, z)$での変位$(u, v, w)$を用いて考える。変化率は下記の変形勾配テンソルで表される。 \[ \left( \begin{array}{ccc} \frac{\partial u_x}{\partial x} & \frac{\partial u_x}{\partial y} & \frac{\partial u_x}{\partial z} \\ \frac{\partial u_y}{\partial x} & \frac{\partial u_y}{\partial y} & \frac{\partial u_y}{\partial z} \\ \frac{\partial u_z}{\partial x} & \frac{\partial u_z}{\partial y} & \frac{\partial u_z}{\partial z} \end{array} \right) \tag{15} \] 天下り的にこれを分解すると、 \begin{align*} \left( \begin{array}{ccc} \frac{\partial u_x}{\partial x} & \frac{\partial u_x}{\partial y} & \frac{\partial u_x}{\partial z} \\ \frac{\partial u_y}{\partial x} & \frac{\partial u_y}{\partial y} & \frac{\partial u_y}{\partial z} \\ \frac{\partial u_z}{\partial x} & \frac{\partial u_z}{\partial y} & \frac{\partial u_z}{\partial z} \end{array} \right) &= \left( \begin{array}{ccc} \frac{\partial u_x}{\partial x} & \frac{1}{2}\left(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x}\right) \\ \frac{1}{2}\left(\frac{\partial u_y}{\partial x}+\frac{\partial u_x}{\partial y}\right) & \frac{\partial u_y}{\partial y} & \frac{1}{2}\left(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y}\right) \\ \frac{1}{2}\left(\frac{\partial u_z}{\partial x}+\frac{\partial u_x}{\partial z}\right) & \frac{1}{2}\left(\frac{\partial u_z}{\partial y}+\frac{\partial u_y}{\partial z}\right) & \frac{\partial u_z}{\partial z} \end{array} \right) + \left( \begin{array}{ccc} 0 & \frac{1}{2}\left(\frac{\partial u_x}{\partial y}-\frac{\partial u_y}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial u_x}{\partial z}-\frac{\partial u_z}{\partial x}\right) \\ \frac{1}{2}\left(\frac{\partial u_y}{\partial x}-\frac{\partial u_x}{\partial y}\right) & 0 & \frac{1}{2}\left(\frac{\partial u_y}{\partial z}-\frac{\partial u_z}{\partial y}\right) \\ \frac{1}{2}\left(\frac{\partial u_z}{\partial x}-\frac{\partial u_x}{\partial z}\right) & \frac{1}{2}\left(\frac{\partial u_z}{\partial y}-\frac{\partial u_y}{\partial z}\right) & 0 \end{array} \right) \\ &=[e_{ij}]+[w_{ij}] \tag{16} \end{align*} 第一項が歪テンソルであり、第二項が回転テンソルである。 \begin{align*} e_{ij}&=\frac{1}{2}\left(\frac{\partial u_i}{\partial j}+\frac{\partial u_j}{\partial i}\right) \tag{17} \\ w_{ij}&=\frac{1}{2}\left(\frac{\partial u_i}{\partial j}-\frac{\partial u_j}{\partial i}\right) \tag{18} \end{align*}

歪テンソルの幾何学的意味を考える。点$A,\ B,\ C$が変形によって図６のように点$A',\ B',\ C'$に移動する場合を考える。 線分ABの$x$軸方向の単位長さあたりの変化量は \[ \frac{\Delta u_x}{\Delta x} =\frac{(\overline{A'B'}-\overline{AB})_x}{\Delta x}=\left\{\left(\Delta x+\frac{\partial u_x}{\partial x}\Delta x\right)-\Delta x\right\}\frac{1}{\Delta x}=\frac{\partial u_x}{\partial x}=e_{xx} \tag{19} \] $y$軸でも同様に考えると$e_{yy}$となる。このことから、歪テンソルの対角成分は、ある線分が同じ方向に変化するときの変化率を示す。この変化率を軸歪と呼ぶ。

線分ABの角度変化$\alpha$は、微小変形を仮定すると$\frac{\partial u_x}{\partial x}\ll 1,\ \tan\alpha\approx\alpha$なので、 \begin{align*} \tan\alpha&=\frac{\frac{\partial u_y}{\partial x}\Delta x}{\Delta x+\frac{\partial u_x}{\partial x}\Delta x} =\frac{\frac{\partial u_y}{\partial x}\Delta x}{\left(1+\frac{\partial u_x}{\partial x}\right)\Delta x}=\frac{\partial u_y}{\partial x} \\ \alpha &=\frac{\partial u_y}{\partial x} \tag{20} \end{align*} 線分ACの角度変化$\beta$も同様にすると、$\beta=\frac{\partial u_x}{\partial y}$なので、 \[ \alpha +\beta=\frac{\partial u_y}{\partial x}+\frac{\partial u_x}{\partial y}=2e_{xy} \tag{21} \] つまり、 \[ e_{xy}=\frac{1}{2}(\alpha+\beta) \tag{22} \] したがって、歪テンソルの非対角成分は、変形により生じる角度変化の半分に対応する。この成分をせん断歪と呼ぶ。

ここで、$\alpha=0$の場合を考える。 \[ e_{xy}=\frac{1}{2}\frac{\partial u_x}{\partial y}=\frac{1}{2}\tan\beta \tag{23} \] 工学的せん断歪$\gamma_{ij}$は$2e_{ij}$なので、 \[ \gamma_{ij}=\tan\beta \tag{24} \] 微小変形を仮定して、式(23)と(24)を導出しているが、式(24)に関しては、そもそも工学せん断歪の定義より自明でもある。

有限歪理論（大変形）では上記のような仮定は使えない。

応力と歪みの関係

応力（空間）と歪（空間）の関係を表したものが構成方程式である。2階のテンソルである応力と歪を結びつけるのが4階のテンソルである弾性定数$C_{ijkl}$。 \[ \sigma_{ij}=C_{ijkl}\varepsilon_{kl} \tag{25} \] 弾性定数は$C_{1111},\ C_{1112},\ C_{3333}$の81成分を持つが、対称性を考えると独立な成分は21個となる。物質が完全な等方弾性体であるとすると、独立な成分は2個のみとなり、クロネッカーのデルタ$\delta$を用いて次のように書ける。 \[ C_{ijkl}=\lambda\delta_{ij}\delta_{kl}+\mu(\delta_{ik}\delta_{jl}+\delta_{il}\delta_{jk}). \tag{26} \] ここで、$\lambda$はラメの第一定数、$\mu$は剛性率である。等方弾性体における弾性定数は他にも、ヤング率$E$、ポアソン比$\nu$、体積弾性率$K$があるが、5つの弾性定数はそれぞれ2つを用いれば表すことができる（表1）。

表1：等方弾性体における弾性定数の相関関係

\begin{array}{c|ccccc} & E & \mu & \lambda & K & \nu \\ \hline E,\ G & E & \mu & \frac{\mu(E-2\mu)}{3\mu-E} & \frac{E\mu}{3(3\mu-E)} & \frac{E-2\mu}{2\mu} \\ E,\ K & E & \frac{3EK}{9K-E} & \frac{3K(3K-E)}{9K-E} & K & \frac{3K-E}{6K} \\ E,\ \nu & E & \frac{E}{2(1+\nu)} & \frac{\nu E}{(1+\nu)(1-2\nu)} & \frac{E}{3(1-2\nu)} & \nu \\ \lambda,\ \mu & \frac{\mu(3\lambda+2\mu)}{\lambda+\mu} & \mu & \lambda & \frac{3\lambda+2\mu}{3} & \frac{\lambda}{2(\lambda+\mu)} \\ \mu,\ K & \frac{9K\mu}{3K+\mu} & \mu & \frac{3K-2\mu}{3} & K & \frac{3K-2\mu}{6K+2\mu} \\ \mu,\ \nu & 2(1+\nu)\mu & \mu & \frac{2\nu\mu}{1-2\nu} & \frac{2(1+\nu)\mu}{3(1-2\nu)} & \nu \\ K,\ \nu & 3K(1-2\nu) & \frac{(3-6\nu)K}{2(\nu+1)} & \frac{3\nu K}{1+\nu} & K & \nu \end{array}

ヤング率$E$は線形弾性体における同軸方向の応力と歪の比例定数である。 \[ \sigma=E\varepsilon \tag{27} \] 剛性率$\mu$は線形弾性体における同軸方向のせん断応力とせん断歪の比例定数である。 \[ \tau=\mu \gamma \tag{28} \] ポアソン比$\nu$は、物体に応力を加えたときに、印加方向と垂直に発生する歪と水平方向に発生する歪の比を取ったものである。例えば、 \[ \nu_x=-\frac{\varepsilon_x}{\varepsilon_z} \tag{29} \] 体積弾性率$K$は、平均応力と体積歪の比例定数である。 \[ \frac{\sigma_{ii}}{3}=K\varepsilon_{ii} \tag{30} \]

応力－歪曲線

ひずみ速度が一定の岩石の変形実験を行うと、応力ひずみ曲線が得られる（図8）。初め、応力と歪の関係は一定であり、岩石は弾性変形をしている（①）。しかしながら、応力が岩石の降伏強度$\sigma_Y$より大きくなると、応力と歪みの関係は一定でなくなり、岩石は塑性変形し始める（②）。更に応力を加え、流動応力$\sigma_F$よりも応力が大きくなると、岩石は一定の流動応力で粘性変形する（③）。塑性変形と粘性変形の違いは、塑性変形は時間に依存しないが、粘性変形は時間に依存する。したがって、粘性変形における流動則（クリープ則）には時間に関連するひずみ速度$\dot{\varepsilon}$が項として入っている。

参考文献

1. [1]「弾性体力学―変形の物理を理解するために― 」中島 淳一・三浦 哲（著）
2. [2]「地球のテクトニクスII 構造地質学」金川 久一 (著)