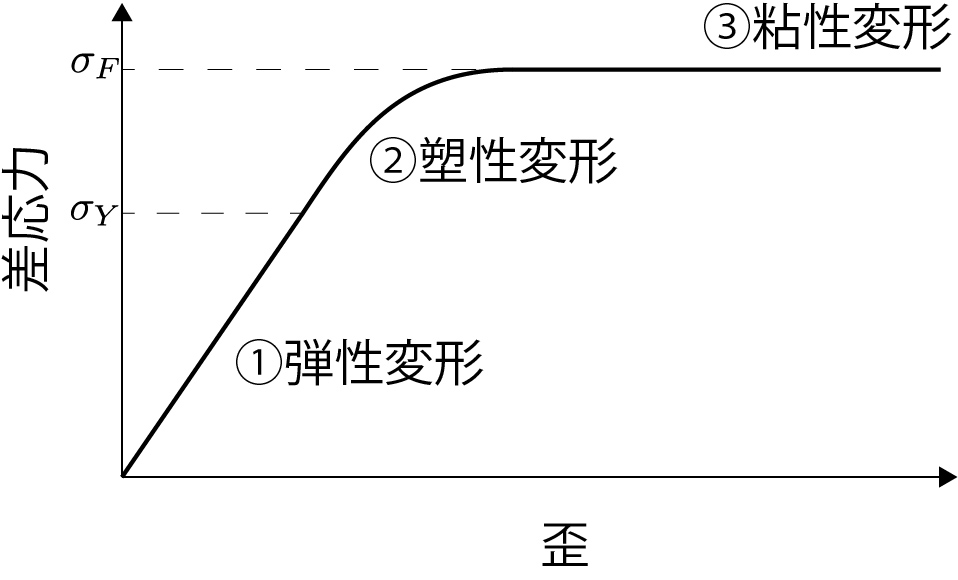
応力
応力は単位面積に作用する力として定義される。 このとき、力はベクトル量なので、応力もベクトルである。 したがって、任意の面に応力$S$が作用している場合、$S$は面に垂直に作用する成分($\sigma$:垂直応力)と平行に作用する成分($\tau$:剪断応力)に分解することができる。
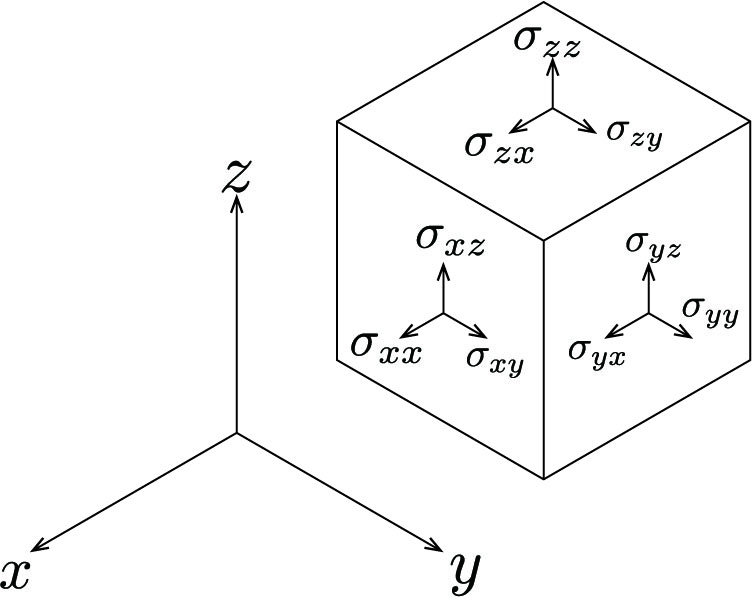
直交座標系において同様に応力を分解すると図1のようになる。垂直応力$\sigma_x$の添字$x$は応力が作用する方向を表す。 一方、剪断応力$\tau_{xy}$の最初の添字$x$は応力の作用する面の法線方向を表し、2番目の添字は応力の作用する方向を表している。 この応力は以下のように行列表記をすることができ、これを応力テンソルと呼ぶ。 \[ S=\left( \begin{array}{ccc} \sigma_x & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_y & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_z \end{array} \right) \tag{1} \]
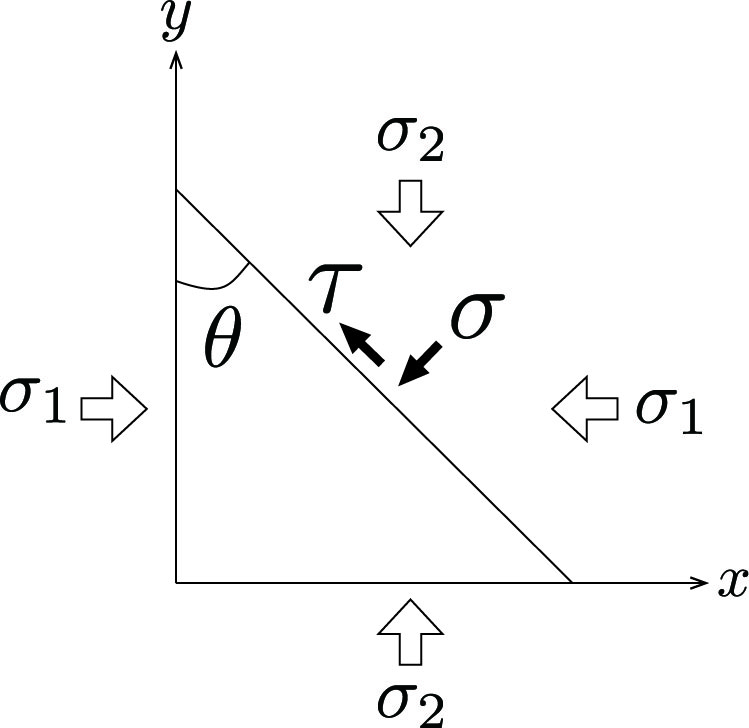
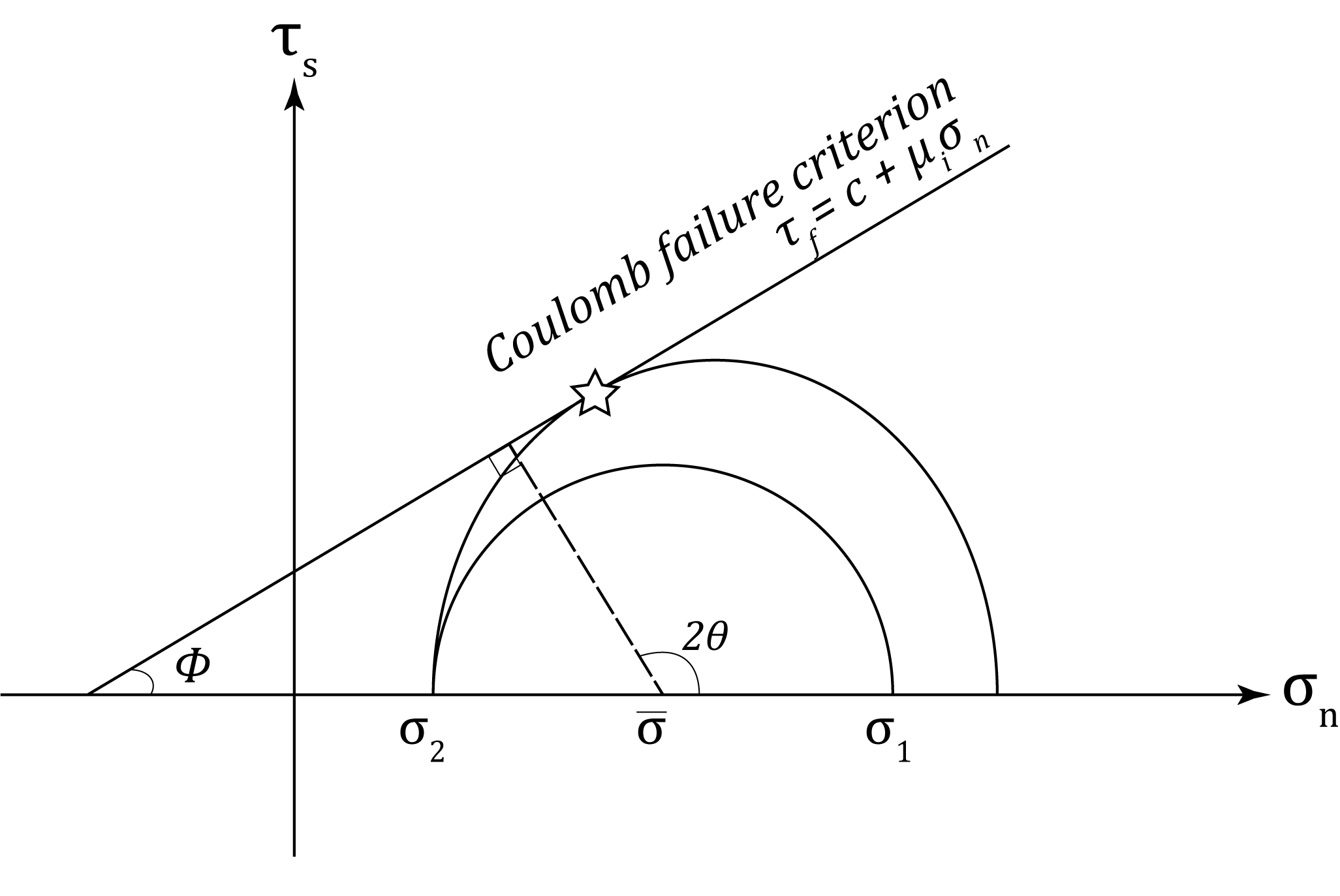
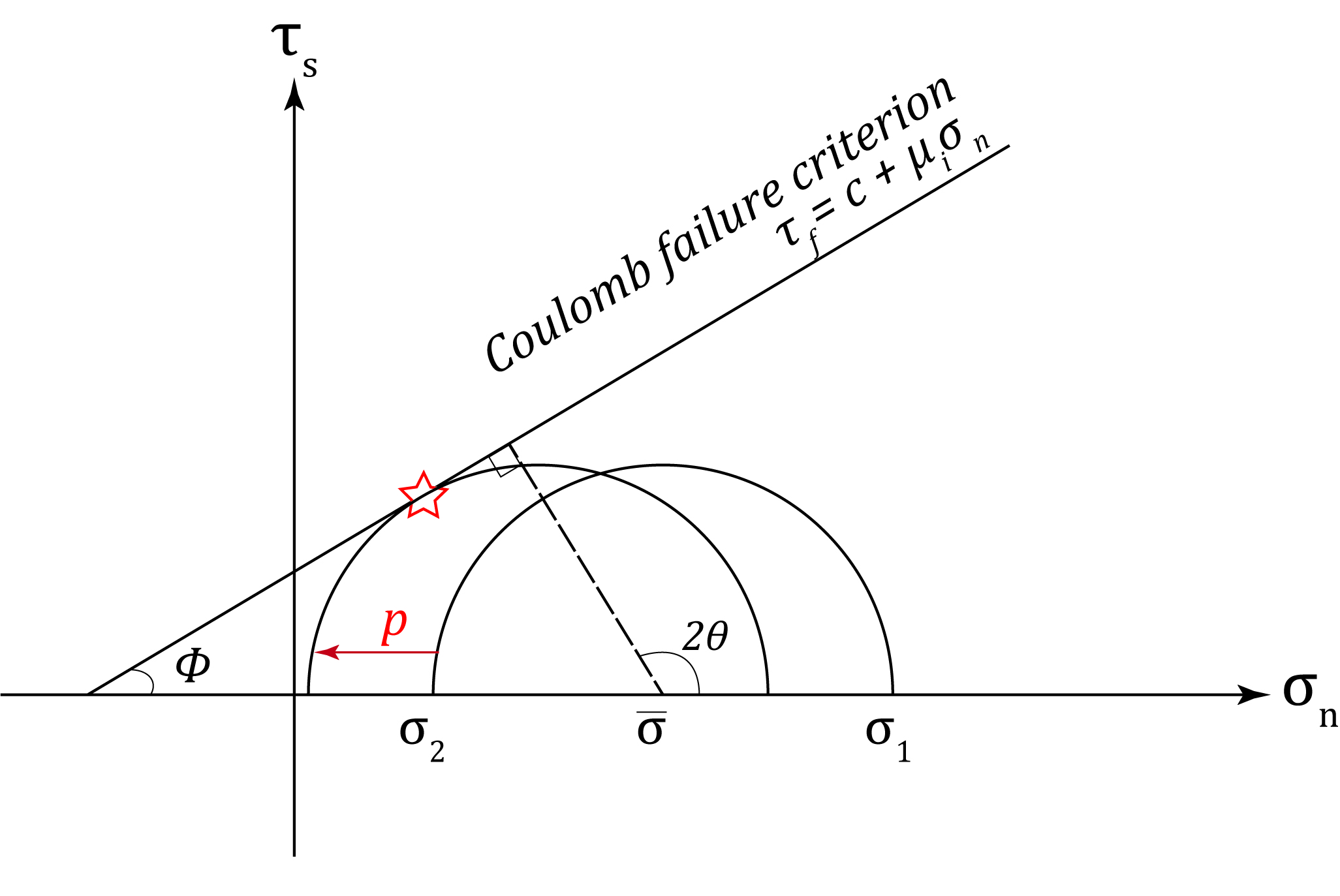
剪断応力成分が0となるように座標系をとったときの垂直応力のことを主応力と呼ぶ。 3つの主応力を$\sigma_1\ge\sigma_2\ge\sigma_3$になるようにとったとき、$\sigma_1$を最大主応力、$\sigma_2$を中間主応力、$\sigma_3$を最小主応力と呼ぶ。 ある座標系で、とある応力状態($\sigma_x, \sigma_y, \sigma_z, \tau_xy, \tau_yz, \tau_zx$)が与えられたとき、 主応力は下記の式を展開した$\lambda$に関する3次方程式の根である。 \[ \mathrm{det}(\sigma-\lambda E)=\left| \begin{array}{ccc} (\sigma_x-\lambda) & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & (\sigma_y-\lambda) & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & (\sigma_z-\lambda) \end{array} \right| \tag{2} \]
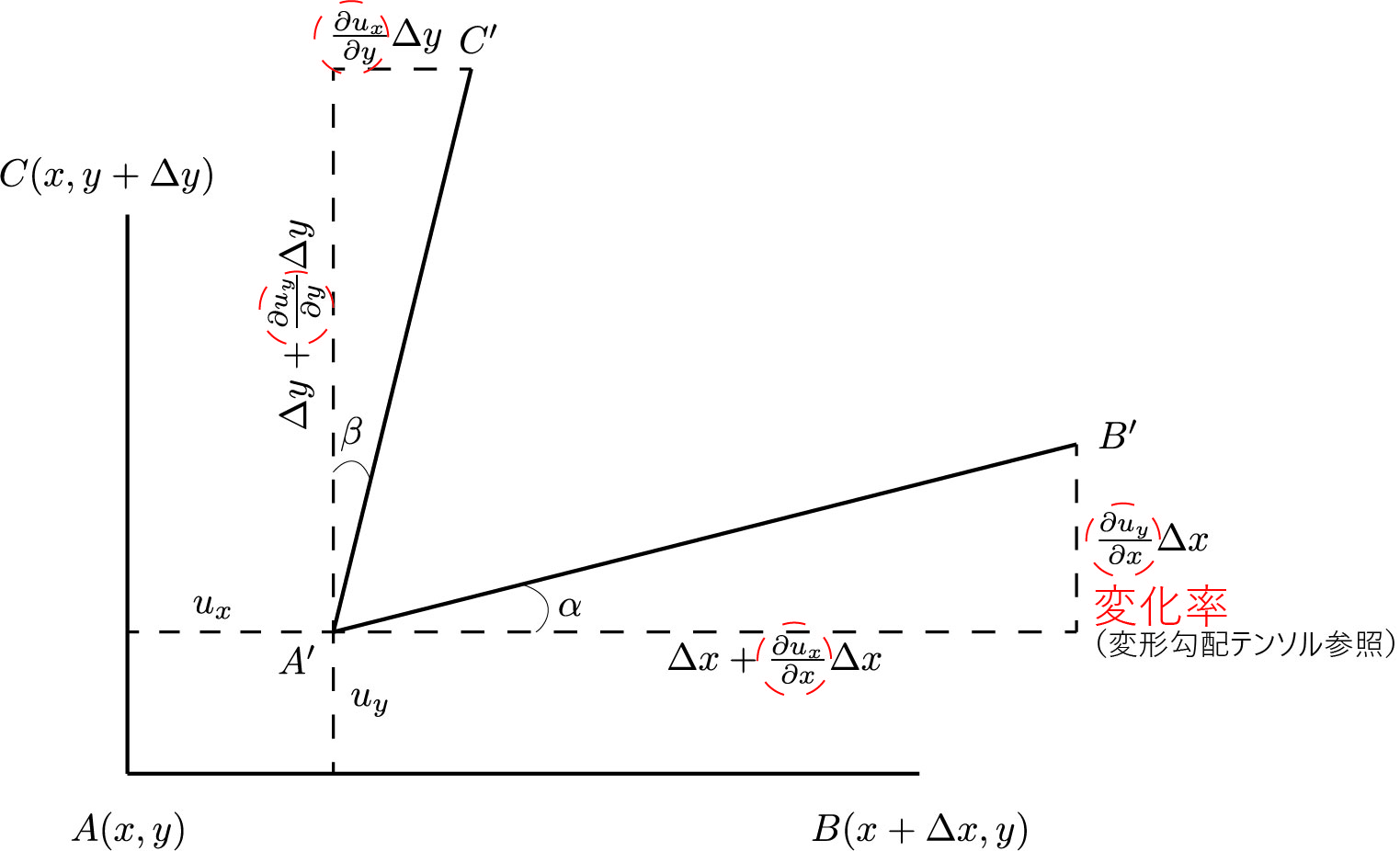
弾性体が平衡状態にあるとき、応力テンソル$\sigma_{ij}$と体積力$F_i$の関係は次の式のようになる。 \[ \sigma_{ji,j}+F_i=0 \tag{3} \] 式(3)を導出するためには$(0,0,0), (dx,0,0), (dx,dy,0), (0,dy,0), (0,dy,dz), (dx,dy,dz), (dx,0,dz), (0,0,dz)$を頂点とする微小直方体を考え、各軸方向の式のつりあいを求める。
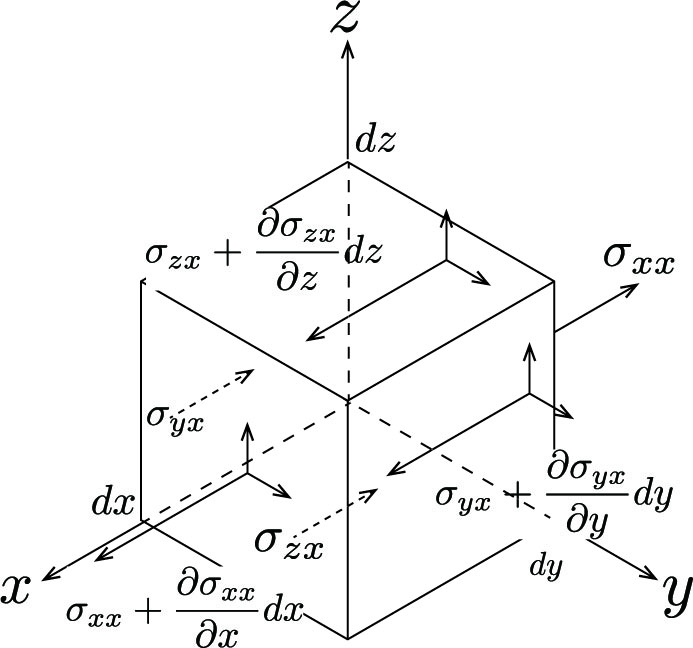
x軸方向における応力成分は図2のようになる。偏微分$\partial \sigma_{xx}/\partial x$は単位距離当たりの変化量を表す。したがって距離をかけてあれば離れた面での応力がわかる。 x軸方向の釣り合いの式は、体積力$F_x$が作用していることを考慮して、 \[ \left(\sigma_{xx}+\frac{\partial \sigma_{xx}}{\partial x}dx\right)dydz-\sigma_{xx}dydz +\left(\sigma_{yx}+\frac{\partial \sigma_{yx}}{\partial y}dy\right)dzdx-\sigma_{zx}dzdx +\left(\sigma_{zx}+\frac{\partial \sigma_{zx}}{\partial z}dx\right)dxdy-\sigma_{zx}dxdy +F_x dxdydz=0 \tag{4} \] 整理すると、 \[ \frac{\partial \sigma_{xx}}{\partial x}+\frac{\partial \sigma_{yx}}{\partial y}+\frac{\partial \sigma_{zx}}{\partial z}+F_x=0 \tag{5} \] y軸、z軸も同様で、総和規約と$\frac{\partial \sigma_{ji}}{\partial x_j}=\sigma_{ji,j} (x_1=x, x_2=y, x_3=z)$より、式(3)が求まる。
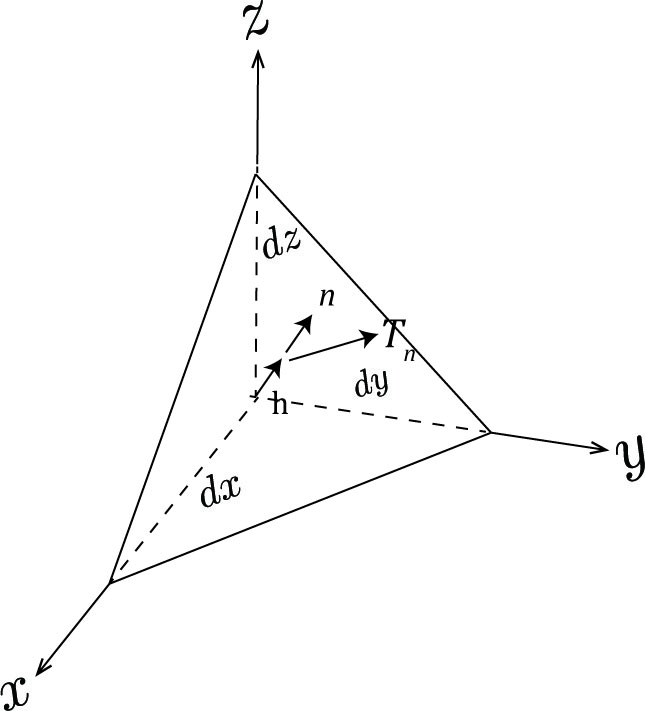
応力テンソル$\sigma_{ij}$が与えられたとき、法線ベクトルが$n$である面(面積:$dS$)に作用する応力ベクトル$T_i$は、 \[ T_i=\sigma_{ij}n_j \tag{6} \] 式(6)をコーシーの関係式と呼ぶ。微小4面体の体積は$dS\cdot h/3$なので、体積力を$F$とするとx方向にかかる体積力による力は$F_x dS\cdot h/3$となる。 また、$yz$面、$zx$面、$xy$面の面積はそれぞれ、$dS\cdot n_x$、$dS\cdot n_y$、$dS\cdot n_z$なので、微小4面体におけるx軸方向の力の釣り合いは、 \[ T^n_xdS+F_x\cdot \frac{1}{3}dS\cdot h=\sigma_{xx}dS\cdot n_x+\sigma_{yy}dS\cdot n_y+\sigma_{zz}dS\cdot n_z \tag{7} \] 微小4面体なので$h\rightarrow0$である。したがって、 \[ T^n_x=\sigma_{xx}n_x+\sigma_{yy}n_y+\sigma_{zz}n_z \tag{8} \] $y$軸、$z$軸も同様で、総和規約を用いると式(6)が求まる。